4973. Мутация

Учёные генетики с планеты Олимпия снова проводят эксперименты с ДНК примитивных организмов. Геном организма представляет собой последовательность генов, каждый из которых можно закодировать с помощью одного натурального числа. Гены, которые кодируются одинаковыми числами, считаются одинаковыми, а гены, кодируемые различными числами, — разными.

Учёные уже создали примитивный организм и хотят модифицировать его геном таким образом, чтобы получить идеальный организм. Они считают, что в будущем это поможет разработать лекарства от множества болезней.

Организм считается идеальным, если любые два одинаковых гена либо находятся на соседних позициях в геноме, либо между ними есть хотя бы один такой же ген.

За одну операцию учёные могут выбрать один или несколько одинаковых генов в геноме, удалить их, а затем вернуть их обратно в геном, возможно, на другие позиции. Поскольку каждая такая операция ослабляет организм, учёные стремятся минимизировать их количество при достижении цели.

Напишите программу, которая по заданному представлению генома определит наименьшее количество операций, необходимых для получения идеального организма.

Вход. Первая строка содержит количество генов n (1 ≤ n ≤ 10⁵) в геноме примитивного организма. Во второй строке записано n натуральных чисел, каждое из которых не превышает n – последовательность генов в геноме.

Выход. Выведите наименьшее количество операций, необходимых для получения идеального организма.

Пример входа	Пример выхода
9 1 2 1 3 1 3 2 4 5	2

РЕШЕНИЕ

жадность

Анализ алгоритма

Перестановку генов следует выполнить таким образом, чтобы одинаковые гены располагались рядом. При этом необходимо минимизировать количество выполненных операций.

Каждому натуральному числу a_i поставим в соответствие отрезок [s_i; e_i], где s_i – позиция, на которой a_i встречается впервые, а e_i – позиция, на которой a_i встречается в последний раз.

Пусть res – наибольшее возможное количество непересекающихся отрезков. Это значение можно найти с помощью алгоритма “выбора заявок”, что означает, что каждый из оставшихся отрезков пересекается хотя бы с одним из выбранных. После этого нужно выполнить описанную процедуру над генами, которым эти отрезки соответствуют.

Если k – общее количество построенных отрезков. Тогда ответом на задачу будет значение k – res.

Пример

Для приведенного примера отрезки будут иметь вид (нумерация позиций начинается с нуля):

· для 1: [0; 4];

· для 2: [1; 6];

· для 3: [3; 5];

· для 4: [7; 7];

· для 5: [8; 8];

Отсортируем отрезки по координате конца:

[0; 4], [3; 5], [1; 6], [7; 7], [8; 8]

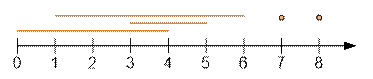
Максимальное количество непересекающихся отрезков равно 3. Например, можно выбрать отрезки [0; 4], [7; 7], [8; 8]. Для генов, соответствующих оставшимся отрезкам, следует выполнить процедуру, описанную в условии задачи. К таким генам относятся 2 и 3. Две перестановки можно выполнить, например, следующим образом:

Реализация алгоритма

Пусть MAX – максимальное возможное количество геномов во входной последовательности.

#define MAX 100001

Вектор пар v хранит отрезки [s_i; e_i].

vector<pair<int, int> > v;

int s[MAX], e[MAX];

Читаем входные данные. Инициализируем s[i] = -1, e[i] = -1.

scanf("%d", &n);

memset(s, -1, sizeof(s));

memset(e, -1, sizeof(e));

for (i = 0; i < n; i++)

{

scanf("%d", &x);

Если число x встречается впервые, то его позицию во входной последовательности записываем в s[x].

if (s[x] == -1) s[x] = i;

Если число x встречается не в первый раз, то его позицию записываем в e[x], считая, что x встречается в последний раз.

if (i > e[x]) e[x] = i;

}

Все построенные отрезки заносим в вектор v.

for (i = 1; i <= n; i++) // numbers 1..n

if (s[i] != -1) v.push_back(make_pair(e[i], s[i]));

Отрезки заносятся в вектор в обратном порядке (в виде [e_i; s_i]), чтобы по умолчанию сортировка отрезков происходила в порядке возрастания их концов.

sort(v.begin(), v.end());

Находим максимальное количество res непересекающихся отрезков.

i = res = 0;

while (i < v.size())

{

Добавляем i-й отрезок во множество непересекающихся отрезков. Переменная temp содержит конец этого отрезка (назовём его текущим отрезком).

res++; temp = v[i++].first; // end

Пока начало следующего отрезка меньше конца текущего, пропускаем такой отрезок, так как он пересекается с текущим.

while (i < v.size() && v[i].second < temp) i++;

}

Выводим ответ.

printf("%d\n", v.size() - res);